Page 1 - Komşu tümler Bütünler Açı-

MATEMATİK KOMŞU, TÜMLER, BÜTÜNLER VE TERS AÇILAR

ÖZET

Komşu, Tümler, Bütünler ve Ters Açılar

Komşu Açılar
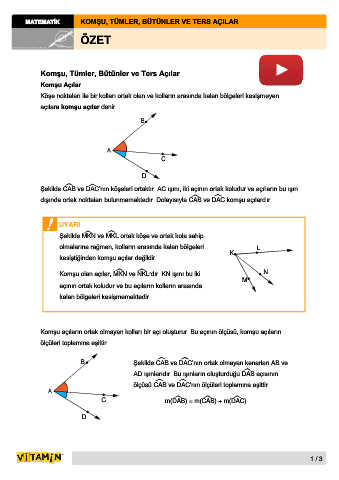
Köşe noktaları ile bir kolları ortak olan ve kolların arasında kalan bölgeleri kesişmeyen

açılara komşu açılar denir.

B

A

C

D

Şekilde CAB ve DAC’nın köşeleri ortaktır. AC ışını, iki açının ortak koludur ve açıların bu ışın
dışında ortak noktaları bulunmamaktadır. Dolayısıyla CAB ve DAC komşu açılardır.

UYARI
Şekilde MKN ve MKL ortak köşe ve ortak kola sahip

olmalarına rağmen, kolların arasında kalan bölgeleri
K L
kesiştiğinden komşu açılar değildir.

Komşu olan açılar, MKN ve NKL dır. KN ışını bu iki N
’
M
açının ortak koludur ve bu açıların kolların arasında

kalan bölgeleri kesişmemektedir.

Komşu açıların ortak olmayan kolları bir açı oluşturur. Bu açının ölçüsü, komşu açıların
ölçüleri toplamına eşittir.

B Şekilde CAB ve DAC’nın ortak olmayan kenarları AB ve

AD ışınlarıdır. Bu ışınların oluşturduğu DAB açısının

ölçüsü CAB ve DAC’nın ölçüleri toplamına eşittir.
A

C m(DAB) = m(CAB) + m(DAC)

D

1 / 3